Maha Bodhi Sch 2007 PSLE Math Prelim Q42

During a sale, a departmental store offered a storewide discount of a certain fixed percentage. Mrs Goh paid for $16 for a dress during the sale and saved $4.
a) What is the percentage discount?
b) How much did Mrs Goh save if she paid $20 for her purchases during the sale?

Solution

a)
Saved ----- $4
Price before discount ----- $4 + $16 = $20
Percentage discount ----- ($4 / $20) x 100% = 20% (Answer)

b)
Price at 80% ----- $20 (after 20% discounted)
10% ----- $20 divided by 8 = $2.50
20% discount ----- $2.50 x 2 = $5

Answer: She saved $5

Maha Bodhi Sch 2007 PSLE Math Prelim Q41

Tom tied his pen to his pencil as shown in the diagram below to form a toy. The length of the pencil is 3/5 the length of the pen. What is the length of the toy?



Solution


2 units ----- 7 cm
1 unit ----- 7 cm divided by 2 = 3.5 cm
Length of toy ----- pen + 3 cm
5 units + 3 cm
(5 x 3.5 cm) + 3 cm = 20.5 cm

Answer: The length of the toy is 20.5 cm

Henry Park Pri Sch 2007 PSLE Math Prelim Q48

A lorry, a van and a car set off at the same time travelling at a constant speed of 60 km/h, 80 km/h and 120 km/h respectively. The lorry and the van were travelling from Town G to Town H while the car was travelling from Town H to Town G. The car passed the lorry 2 minutes after passing the van.
a) Find the ratio of the distances travelled by the lorry to the van to the car at the moment when the car passed the van.
b) Find the distance between Town G and H.

Solution

a)
Since all of them started at the same time, the distance covered by each vehicle is proportionate to their respective speeds.

Lorry : Van : Car
60 : 80 : 120
3 : 4 : 6 (Answer)

b)
Ratio of the distance covered by the lorry to the distance covered by the car is 3:6 or 1:2. Hence, for every 2 units of distance the car travelled, the lorry travelled 1 unit.

Ratio of distance covered by the van to the distance covered by the car is 4:6 or 2:3. Hence, for every 3 units of distance the car travelled, the van travelled 2 units.



Van covered 2 units for every 3 units car covered.
Hence if the van covered 6 units, the car would have covered 9 units.

Lorry covered 1 unit for every 2 units car covered.
Hence, if the lorry covered 5 units, the car would have covered 10 units.

Distance = speed x time

The speed of the car was 120 km/h.
When the car passed the lorry, it was 2 min after it had passed the van.

Distance covered by the car within those 2 minutes ----
120 km/h x 1/30 h = 4 km

1 unit ----- 4 km

(Total distance)
15 units ----- 4 km x 15 = 60 km

Answer: The distance between Towns G and H is 60 km.

Henry Park Pri Sch 2007 PSLE Math Prelim Q47

At first, Bob had only $5-notes and Chris had only $2-notes. The number of notes Bob had is 80% of Chris’ notes. When Bob gives Chris $100, the number of notes Chris has now is 70% more than Bob.
a) How many notes did Bob have at first?
b) How much money does Chris have at the end?

Solution

a) When Bob gave $100 to Chris, Bob gave Chris 20 notes because Bob had only $5 notes ----- $100 divided by $5 notes = 20 $5-notes.




(Bob) 136% - 34 notes ----- 100% + 20 notes (Chris)
136% - 100% ----- 34 notes + 20 notes
36% ----- 54 notes
1 % ----- 54 divided by 36 = 1.5
80% ----- 1.5 x 80 = 120

Answer: Bob had 120 notes at first.

b) Chris had at the end ----- (100%) + 20 notes

100% ----- 100 x 1.5 = 150 (notes)
150 notes x $2 = $300

20 notes x $5 (given by Bob)
= $100

$300 + $100 = $400

Answer: Chris had $400 in the end.

Henry Park Pri Sch 2007 PSLE Math Prelim Q46

In the figure, ABCD is a square with a perimeter of 84 cm. It is made up of identical squares and quarter-circles.
a) Find the perimeter of the shaded region.
b) Find the area of the shaded region.



Solution

a)
The perimeter of square ABCD is 84 cm.
1 side of square ABCD ----- 84 cm divided by 4 = 21 cm
Radius of the 6 quadrants ----- 21 cm divided by 3 = 7 cm

The shaded area is made up of 6 quadrants -----
6 x ¼ x 2 x 22/7 x 7 cm = 66 cm (Answer)


b) Redrawing the figure….


Area of 1 quadrant -----
¼ x 22/7 x 7 cm x 7 cm = 38.5 square cm

Area of 1 small partially shaded square ----
Area of 1 small square – Area of 1 quadrant ----- (7 cm x 7 cm) – 38.5 square cm = 10.5 square cm

Area of 2 such small partially shaded squares -----
10.5 square cm x 2 = 21 square cm

Area of 3 small shaded squares -----
(3 x 7 x 7) square cm = 147 square cm

Total shaded area ------
(21 + 147) square cm = 168 square cm (Answer)

Henry Park Pri Sch 2007 PSLE Math Prelim Q45

Terrence earns $350 less than Leslie every month. They each spend $800 every month and save the rest of their money.
a) How long does it take for Terrence to save $2100 and Leslie to save $4550?
b) What is Terrence’s monthly salary?

Solution



a) (Leslie's savings) – (Terrence’s savings) -----
$4550 - $2100 = $2450

$2150 divided by $350 (per month) ----- 7 months

Answer: It takes 7 months.

b) In 7 months, Terrence saves $2100
1 month ----- $2100 divided by 7 = $300

Terrence’s salary ----- $800 + $300 = $1100

Answer: Terence’s monthly salary is $1100.

Henry Park Pri Sch 2007 PSLE Math Prelim Q44

Study the diagram below.
a) What is the sum of Angle a, Angle b, Angle c, Angle d, Angle e and Angle f?


Solution

Angles on a straight line = 180 degrees
3 straight lines will have a total of 180 degrees x 3 = 540 degrees
Sum of all Angles a to f -----
540 degrees – sum of angles of triangle
= (540 – 180) degrees
= 360 degrees (Answer)


The figure below shows a rectangle and a triangle.
b) What is the sum of Angle p + Angle q?


Solution

Sum of interior angles of 2 parallel lines ----- 180 degrees (Answer)

Henry Park Pri Sch 2007 PSLE Math Prelim Q43

Four children, Angela, Belinda, Cristobel and Dorothy shared $240. Angela received ½ of the total amount of money received by Belinda, Cristobel and Dorothy. Belinda received 2/3 of the total amount of money received by Cristobel and Dorothy. Cristobel received 3 times as much money as Dorothy.
a) How much money did Dorothy receive?
b) What fraction of Angela’s money is Dorothy’s money if Angela gave $20 to Dorothy?

Solution



10 units ----- $240
1 unit ----- $240 divided by 10 = $24

a) Dorothy
1 unit ----- $24.

Answer: Dorothy received $24.

b) (Angela) 3 1/3 units ----- $24 x 3 1/3 = $80
(Dorothy) 1 unit ----- $24
If Angela gives Dorothy $20,
Angela ----- $80 – $20 = $60
Dorothy ----- $24 + 20 = $44
$44 / $60 = 11/15 (Answer)

Henry Park Pri Sch 2007 PSLE Math Prelim Q42

At first, the total number of sheep in Farm A and Farm B was 980. After 3/5 of the sheep in Farm A and 200 of the sheep in Farm B are sold, the ratio of the number of sheep in Farm A to Farm B becomes 1 : 4.
a) Find the number of sheep in Farm B at first.
b) Find the total number of sheep left in Farm A and Farm B.

Solution


13 units ----- 980 – 200 = 780
1 unit ----- 780 divided by 13 = 60
a) Number of sheep in Farm B at first -----
8 units + 200 ----- (8 x 60) + 200 = 680

Answer: There were 680 sheep in Farm B at first.

b) Total number of sheep left in Farm A and Farm B -----
10 units ----- 10 x 60 = 600

Answer: There were 600 sheep left in both farms.

Vocabulary - illusion ; allusion

What's this video clip have to do with vocabulary?
Play the clip and read later.



Illusion -
1. something that deceives by producing a false or misleading impression of reality.
2. the state or condition of being deceived; misapprehension.
3.an instance of being deceived.
4.Psychology. a perception, as of visual stimuli (optical illusion), that represents what is perceived in a way different from the way it is in reality.
5. a very thin, delicate tulle of silk or nylon having a cobwebbed appearance, for trimmings, veilings, and the like.
6. Obsolete. the act of deceiving; deception; delusion.

Most students do not have problems understanding what "illusion" is.

"Allusion" however, has a different meaning -
1. a passing or casual reference; an incidental mention of something, either directly or by implication: an allusion to Shakespeare.
2. the act of alluding.
3. Obsolete. a metaphor; parable.

As an example, the video clip above is taken from the 1996 movie, "The Thing That You Do!" It is a fictional movie about a boy-band group set in the 1960s.

What is obvious is that the movie (and the boy-band group) is an allusion to the "Beatlemania era" of the sixties.

Beatlemania is a term that was used during the 1960s to describe the intense fan frenzy (particularly demonstrated by young teenaged girls) directed toward The Beatles, particularly during the early years of their success. A portmanteau of "Beatles" and "mania", it is claimed to have been coined in 1963 by Andi Lothian, a Scottish music promoter, although the first printed use of the word is in The Daily Mirror 2nd November 1963 in a news story about the previous day's Beatles concert in Cheltenham. Many fans across the world were known to have Beatlemania (and were thus known as "Beatlemaniacs") which hit the United States hard after The Beatles performed on The Ed Sullivan Show in 1964. 'Beatlemania' was characterised by intense levels of hysteria demonstrated by fans both during the actual concerts played by the band (during which the level of screaming was often so loud as to completely drown out the music) and during the band's arrivals and travels to and from locations. One can envision the dimensions of the original Beatlemania during its peak year in 1964 by looking at the unprecedented sales figures caused by it. During 1964, The Beatles sold over 30 million records in America alone, at one stage holding the top five positions in the singles chart.

Henry Park Pri Sch 2007 PSLE Math Prelim Q41

In the following figures, the area of the biggest equilateral triangle is 64 square cm as shown in Figure 1. A new triangle is formed by connecting the midpoints of the sides of the previous triangle. If the pattern continues, find the area of the smallest triangle in Figure 4.



Solution

The shaded area of Figure 2 is ¼ of the Area of Figure 1 -----
¼ x 64 square cm = 16 square cm

The shaded area of Figure 3 is ¼ of the shaded area of Figure 2 -----
¼ x 16 square cm = 4 square cm

The shaded area of Figure 4 is ¼ of the shaded area of Figure 3 -----
¼ x 4 square cm = 1 square cm (Answer)

Henry Park Pri Sch 2007 PSLE Math Prelim Q40

There were 30 more members in the IT Club than in the Art Club. 15 members left the Art Club for the IT Club. It was then found that the number of members in the IT Club was 5 times as many as the number of members in the Art Club. How many members were there in both clubs altogether?

Solution



4 units ----- 60
1 unit ----- 60 divided by 4 = 15
(Altogether) 6 units ----- 15 x 6 = 90

Answer: There were 90 members altogether.

Common Mistake - Perimeter of Partial Circles

Henry Park Pri Sch 2007 PSLE Math Prelim Q39

The figure is not drawn to scale. ABCD is a parallelogram. Find Angle ADC.



Solution

Angle AEB = (180 - 58 – 35) degrees = 87 degrees
(Angles in a triangle)

Angle ABC = (87 + 38) degrees = 125 degrees

Angle ADC = 125 degrees (Answer) (Opposite angles of a parallelogram)

Henry Park Pri Sch 2007 PSLE Math Prelim Q37

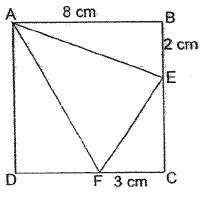
In the figure, ABCD is a square of side 8 cm. BE is 2 cm and FC is 3 cm. Find the area of Triangle AEF.


Solution

Area of Square ABCD ----- 8 cm x 8 cm = 64 square cm
Area of Triangle ABE ----- ½ x 8 cm x 2 cm = 8 square cm
Area of Triangle CEF ----- ½ x 3 cm x 6 cm= 9 square cm
Area of Triangle ADF ----- ½ x 5 cm x 8 cm = 20 square cm

Area of Triangle AEF -----
(64 – 8 – 9 – 20) square cm = 27 square cm (Answer)

Henry Park Pri Sch 2007 PSLE Math Prelim Q36

Joseph has $m. Kenny has 3 times as much money as Joseph. Leo has half the amount of money Joseph and Kenny has altogether. How much money do the 3 boys have altogether?

Solution

Joseph ----- $m
Kenny ----- 3 x $m = $3m
Joseph and Kenny ----- $m + $3m = $4m
Leo ----- $4m divided by 2 = $2m

Total ----- $4m + $2m = $6m

Answer: They had $6m altogether.

S’pore Hokkien Huay Kuan 2007 PSLE Math Prelim Q48

Siti had some red and blue marbles. 80% of the marbles were red. After she bought another 63 red marbles and 46 blue marbles, 75% of the marbles were red. Find the total number of marbles she had at first.

Solution



(8 units – 6 units) + (63 – 138) ----- 75% - 75%
2 units – 75 ----- 0
2 units ----- 75
1 unit ----- 75/2

Total number of marbles at first
10 units ----- 75/2 x 10 = 375

Answer: She had 375 marbles at first.

Note – “The Singapore Hokkien Huay Kuan 5-School Combined Prelim Maths” is the common Maths Prelim Exam for Tao Nan, Ai Tong, Chongfu, Nan Chiau and Kong Hwa schools.

S’pore Hokkien Huay Kuan 2007 PSLE Math Prelim Q47

Ahmad formed the following patterns using toothpicks.





a) How many toothpicks would Ahmad need to form Pattern 4?
b) If the last pattern formed by Ahmad had 165 toothpicks, what was the pattern number?


Solution

a)
Pattern 1 –---- 3
Pattern 2 ----- (3 + 6) = 9
Pattern 3 ----- (6 + 9) = 18
Pattern 4 ----- (18 + 12) = 30

Answer: 30

b)
Pattern 5 ----- (30 + 15) = 45
Pattern 6 ----- (45 + 18) = 63
Pattern 7 ----- (63 + 21) = 84
Pattern 8 ----- (84 + 24) = 108
Pattern 9 ----- (108 + 27) = 135
Pattern 10 ----- (135 + 30) = 165

Answer: Pattern 10

Note – “The Singapore Hokkien Huay Kuan 5-School Combined Prelim Maths” is the common Maths Prelim Exam for Tao Nan, Ai Tong, Chongfu, Nan Chiau and Kong Hwa schools.

S’pore Hokkien Huay Kuan 2007 PSLE Math Prelim Q46

At 8.30 am. Tom drove from Town P to Town Q at an average speed of 80 km/h. After driving 2/5 of the journey for 4 hours, he passed Paul who was travelling along the same road in the opposite direction. Paul was travelling at a speed which was 20 km/h slower than Tom. At what time did Paul leave Town Q?

Solution



2 units ----- 320 km
1 unit ----- 320 km divided by 2 = 160 km

Distance Paul covered when he passed Tom
3 units ----- 160 km x 3 = 480 km

Time Paul took to cover 480 km -----
480 km divided by 60 km/h = 8 hours

8 hours before 12.30 pm is 4.30 am.

Answer: Paul left Town Q at 4.30 am.

Note – “The Singapore Hokkien Huay Kuan 5-School Combined Prelim Maths” is the common Maths Prelim Exam for Tao Nan, Ai Tong, Chongfu, Nan Chiau and Kong Hwa schools.

Free PSLE Aggregate Score Calculator

Excel Eduservice thrives to serve you better. For the first time in Singapore, made available to the public is the PSLE Aggregate Score Calculator.

This software programme is in Microsoft Excel format - and it is made available to you by Excel Eduservice for FREE!

A sample screenshot of the PSLE Aggegate Score Calculator is shown below. Click on the image to enlarge.



Question - How do I get a copy of the PSLE Aggregrate Score Calculator?

Answer - Click here to download.

PS - To understand how PSLE Aggregate scores are calculated, just click here.

=================================
Excel Eduservice
You're in good hands when you're with Excel!
=================================

S’pore Hokkien Huay Kuan 2007 PSLE Math Prelim Q45

An empty tank was filled with water from two taps. Tap A could fill the tank completely in 2 hours and Tap B could fill it completely in 6 hours. Tap A was turned on first and Tap B was turned on 20 minutes later.

a) What fraction of the tank was filled with water after 20 minutes?
b) How long did it take to fill the rest of the tank completely with water?

Solution

a) (Tap A)
2 hours ----- full tank
1 hour ----- half tank
1/3 hour (20 min) ----- 1/3 x ½ tank = 1/6 tank

Answer: 1/6 of the tank would be filled after 20 min.


b) Tap A takes 2 hours to fill tank completely, while Tap B takes 6 hours.
The ratio of the volume that Tap A to Tap B will fill if both taps are on simultaneously is therefore 6 : 2 or 3 : 1.

Volume filled by
Tap A : Tap B
3 : 1

Since 1/6 has been filled at first, there is another 5/6 to be filled after 20 min.

Out of the 5/6 that has to be filled, Tap A will fill ¾ of it, while Tap B will fill ¼ of it. (Since the ratio of volume that will be filled by Tap A : Tap B is 3:1)

Hence, Tap A -----

Full tank ----- 2 hours
5/6 tank ----- 2 x 5/6 hours = 5/3 hours
¾ of 5/6 tank ----- ¾ x 5/3 hours = 5/4 hours or 75 min.

Answer: It will take 75 min to fill the rest of the tank.

Note – “The Singapore Hokkien Huay Kuan 5-School Combined Prelim Maths” is the common Maths Prelim Exam for Tao Nan, Ai Tong, Chongfu, Nan Chiau and Kong Hwa schools.

Tips on PSLE English (Oral)

A video clip produced by Paya Lebar Methodist Girls' School (Primary).

S’pore Hokkien Huay Kuan 2007 PSLE Math Prelim Q44

Cynthia has 32 English and Chinese books. 4/5 of the English books and ¾ of the Chinese books are fiction books. She has a total of 25 fiction books. How many English fiction books are there?

Solution



5 units + 4 parts ----- 32 (Total books)
4 units + 3 parts ----- 25 (Fiction books)

Multiply "Total books" by 3 and
Multiply "Fiction books" by 4, we will have

15 units + 12 parts ----- 96
16 units + 12 parts ----- 100

From the above, we can see that
1 unit ---- 100 – 96 = 4

(English Fiction books) 4 units ---- 4 x 4 = 16

Answer: There are 16 English fiction books

Note – "The Singapore Hokkien Huay Kuan 5-School Combined Prelim Maths" is the common Maths Prelim Exam for Tao Nan, Ai Tong, Chongfu, Nan Chiau and Kong Hwa schools.

S’pore Hokkien Huay Kuan 2007 PSLE Math Prelim Q42

Mrs Lim bought a total of 120 apples and oranges in the ratio of 3 : 5. After she gave away an equal number of each type of fruit, the ratio of the number of apples to the number of oranges left is 3 : 8. How many apples does she have now?

Solution

Apples : Oranges ----- 3 : 5 (Total 120 fruits)

Hence, 8 units ----- 120
1 unit ----- 120 divided by 8 = 15

(Apples) 3 units ----- 15 x 3 = 45
(Oranges) 5 units ----- 15 x 5 = 75



5 units ----- 30
1 unit ----- 30 divided by 5 = 6
(Apples left) 3 units ----- 3 x 6 = 18

Answer: She has 18 apples left.

Note – “The Singapore Hokkien Huay Kuan 5-School Combined Prelim Maths” is the common Maths Prelim Exam for Tao Nan, Ai Tong, Chongfu, Nan Chiau and Kong Hwa schools.

S’pore Hokkien Huay Kuan 2007 PSLE Math Prelim Q43

The figure below is made up of a semicircle and a rectangle. Find the area of the unshaded region.






Solution

The base of the figure is 28 cm. The diameter of the unshaded circle is half the base, hence, it is 14 cm. This also means that the radius of the circle is 7 cm.

The radius of the 2 quadrants is 14 cm.

Area of circle ----- 22/7 x 7 cm x 7 cm = 154 square cm

Area of 1 quadrant ----- 22/7 x 14 cm x 14 cm x ¼ = 154 square cm

Area of 2 quadrants ----- 154 square cm x 2 = 308 square cm

Total unshaded area ----- (154 + 308) square cm

= 462 square cm (Answer)

Note – “The Singapore Hokkien Huay Kuan 5-School Combined Prelim Maths” is the common Maths Prelim Exam for Tao Nan, Ai Tong, Chongfu, Nan Chiau and Kong Hwa schools.

The Simple Present Perfect Tense

The structure of this tense is – “have/has + past participle”

Examples –
Jane has completed her homework.
I have cleaned my room.

Application –
So when do we use the Simple Present Perfect? Why can’t we just use the Simple Past? Let’s compare them.

A) I have cleaned my room. (Simple Present Perfect)
B) I cleaned my room. (Simple Past)

In Example A, the impression we get is that I have just cleaned my room recently. In Example B, there is no time inferred at all. It could mean I cleaned my room yesterday, last week, or even last month.

Generally speaking, the simple present perfect tense (has/have + past participle) is used when the event has taken place recently.


Frequency of Occurrence -

So how recent is recent? A few minutes? Hours? Days? Weeks? Months?

The answer lies in the frequency of the event. Here are more examples, with varying degrees of frequency of occurrence.

1. I have eaten – We eat about 3 times a day. Hence, when I say, “I have eaten”, it means that I have eaten about an hour or two hours ago at most. We don’t say, “have eaten”, if we meant the last meal we had was yesterday.

2. He has gone to school - Going to school is a daily affair. Most of the time, school students go to school once a day. Hence, again, it is quite reasonable to say “has gone to school” if we meant it happened a few hours ago, but not yesterday.

3. She has received her salary – Most salaried employees receive their pay once or twice a month. In this case, we can say “has received her salary”, if we meant it happened a few days ago. Unlike the first two examples, the frequency of occurrence for this event is spread out in a month, and not over a day.

4. He has celebrated his birthday – This is a yearly affair. Hence, it is reasonable to say, “has celebrated his birthday”, if we meant it happened a few weeks ago.

5. Auntie Jen has given birth to a baby girl – Mothers don’t give birth every month. Most don’t give birth even every year. In this case, even if the event occurred a few months ago, we still can say, “has given birth”.

6. We have seen a new millennium – A millennium occurs every 1000 years. The last millennium was the year 2000, and the next will be the year 3000. We are now in the year 2008, and the next millennium will occur 992 years from now. As such, even though the last occurrence happened 8 years ago, we still can say, “We have seen a new millennium.”


Summary

As can be seen from the above examples, the simple present perfect tense can be used for an event that occurred recently. How one judges an event to be "recent" depends on the frequency of the occurrence. In Example 6, the frequency is once every 1000 years, making 8 years “recent”.

However, going to school is an everyday affair and hence, it would not be appropriate and even ridiculous to say, “He has gone to school”, if you meant that event occurred 8 years ago.

S’pore Hokkien Huay Kuan 2007 PSLE Math Prelim Q41

Ali had y stamps. His father gave him 20 more stamps. He then shared all his stamps equally with his 2 brothers.
a) How many stamps did each boy get in terms of y?
b) If y = 28, how many stamps did each boy get?

Solution

a)
Number of stamps Ali had at first ----- y
After father gave another 20 stamps ----- y + 20
After sharing with 2 other brothers ----- (y + 20) divided by 3
= (y + 20)/3 (Answer)

b) If y = 28 -----
(28 + 20)/3 stamps
= 48/3 stamps
= 16 stamps (Answer)

Note – “The Singapore Hokkien Huay Kuan 5-School Combined Prelim Maths” is the common Maths Prelim Exam for Tao Nan, Ai Tong, Chongfu, Nan Chiau and Kong Hwa schools.

S’pore Hokkien Huay Kuan 2007 PSLE Math Prelim Q40

A bottle of cooking oil weighs 2 kg. A hawker uses 8 such bottles in 4 days. If he uses the same amount of oil every day, how many 5-kg tins of cooking oil will he use in 10 days?

Solution

1 bottle ----- 2 kg
8 bottles ----- 2 kg x 8 = 16 kg (for 4 days)

1 day ----- 16 kg divided by 4 = 4 kg (per day)
10 days ----- 4 kg x 10 = 40 kg

If 5-kg tins were used ----- 40 kg divided 5 kg = 8

Answer: He would use 8 5-kg tins in 10 days.

Note – “The Singapore Hokkien Huay Kuan 5-School Combined Prelim Maths” is the common Maths Prelim Exam for Tao Nan, Ai Tong, Chongfu, Nan Chiau and Kong Hwa schools.