Catholic High School P5 CA1 2004 Math Question

Mr Tan had thrice as many apples as pears at his stall at first. After he sold 129 apples and threw away 8 rotten pears, he had only half as many apples as pears left. How many pears did he have left?


Before -



After – Threw 8 pears, sold 129 apples, left with half as many apples as pears.




Apples sold

5 units + 8 + 8 + 8 ----- 129

5 units + 24 ----- 129

5 units ----- 129 –24

5 units ----- 105

1 unit ----- 105 divided by 5 = 21


Pears left

2 units ----- 21 x 2 = 42


Answer: He had 24 pears left.

Past Perfect Tense – The Most Often Misused Tense

The Past Perfect Tense (had + past participle, eg “had eaten”) is the most common misused tense by Singaporeans, students included.

Many of us say, “Mother had gone to the market”. This is grammatically wrong. The correct phrase is “Mother has gone to the market”.

The Past Perfect Tense can only be used when:

Condition 1: Mentioning a past action that has completed before another past action.

Condition 2: Mentioning a past action that has completed before a certain definite time.


Examples

Condition 1: Mentioning a past action that has completed before another past action.




In both Examples A and B, the first action that happened is in the Past Perfect Tense, while the second action that happened after the first, is in the Simple Past.

Condition 2: Mentioning a past action that has completed before a certain definite time.




In both Examples C and D, the action that has completed before a certain definite time, is in the Past Perfect Tense.

Question – Do you know why the sentence “Mother had gone to the market” is incorrect?

As seen from the four examples, the Past Perfect Tense can only be used, when there is another action that followed it, or when we mention an action that happened before a specific time. The sentence “Mother had gone to the market”, has only one action and has no reference to any specific time.

The correct phrase should be, “Mother has gone to the market”. This is the Present Perfect Tense (have/has + past participle). The Present Perfect is used when we mention an action that has recently happened.

How do I motivate the class? Part 1

Disclaimer – This article is written based on my personal experience as a schoolteacher when I was teaching in a public school. It should NOT to be taken as a professional advice site for teachers seeking help.

There are many sites that give tips to students. There are also many sites that give tips to parents with school-going children. Sadly, there are hardly any sites that give teachers advice. Teachers are humans too. Sometimes we forget that they too have their own set of challenges, just like students and parents have theirs.

This post is thus dedicated to teachers – because they are the most important component in the education system.
-------------------------

How do I motivate the class? Part 1

Let’s face it, Teachers. Being an ex-teacher myself, I know that many of you have faced this situation before:- Yes, it had to come. It simply had to. Then one day, it did. The whole class did BADLY. Hardly anyone passed the test - and the one or two who did, barely scraped through.

The question that comes into the mind is – was there something wrong with my teaching?

A fellow teacher notices you. He comes up to you and reassures you that it was “not your fault”. You knew that he meant well. But that still does not erase from your mind that your class did badly and that affects YOUR morale as a teacher.

If your morale dips, your students will sense it. This then goes into a vicious cycle of “low morale begets low morale” between teacher and students.

So, what next?

Teachers, especially new ones, must remember that not all students can ace in every subject. There are high performers, and there are not so high performers. It is glamorous to teach a superstar “A” class. Not that teaching an “A” class has no challenges. It has its own set of challenges - demanding parents, high expectations from your superiors that your students produce results for the school, etc.

On the other hand, teaching a class that consistently produces below par results does affect the morale of the teacher, doesn’t it? So what can you do to ensure that their results improve?


Go for the jugular – Mathematics

From experience, I find that of the 3 core subjects, English, Maths and Science, Mathematics is the one subject that makes or breaks the student’s morale.

Maths (especially at P5 and P6) can appear very intimidating. However, once the student gets the technique right and starts scoring, his morale takes a quantum leap.

Maths is also the only subject that can be improved within 2 or 3 months. Hence, a student who fails his Maths in CA1 with a 40+ score, if guided properly, can produce a 60+ in SA1.

The above is key to motivating the below par performing student. A student who has been failing Maths consistently, will be in cloud nine, if he passes his first Maths Exam after a long time.

Now imagine if just half the class improved their Maths scores by 20 marks within one term. Those who made that improvement will start to believe in themselves and start to pursue better results for other subjects. The other half that did not improve their Maths, will also open their eyes. If their classmates can do it, why not them?

This then causes a chain reaction. The class will start believing in themselves and will somehow start to make effort to improve their scores for all subjects.

The above all sounds too easy, isn’t it? But in real life, it isn’t so easy! But then again, who said life is easy?


So what must be done to get the below par students to improve their Maths by 20 marks within 3 months?

Here are the 3 most common reasons why some students do very badly in PSLE Maths.

1. They do not know their multiplication tables -

Make it a basic requirement that every student must know his multiplication tables. A student who does not have multiplication tables at his fingertips will be seriously disadvantaged.

A P4 student who does not know his multiplication tables will have problems dealing with Factors and Multiples. He will be slowed down finding common multiples. He will be slowed down when dealing with the addition or substraction of fractions, because he cannot see with one glance, what is the common denominator needed to solve the sum. When it comes to multiplication and division of fractions, he cannot see if the numerator and the denominator share a common factor, such that the fraction can be reduced to a simpler form, so that the problem can be solved more easily.

A P5 or P6 student who does not have multiplication tables at his fingertips is a recipe for disaster. The two and one quarter hours allocated for the Maths Exam Paper would not be enough for him. He will go “finger counting” for almost every multiplication and division working he comes across.

I have invigilated exams and I have observed that P5 and P6 students who go “finger counting” during Maths Exams, usually do not have enough time to finish their papers. They leave up to 3 or even 4 pages of questions unanswered. That’s a lot of marks wasted!

Hence, it is critical, that the student must have his multiplication tables at his fingertips.


2. They do not have a strong grasp on the topic of Fractions (including the 4 operations) -

At P5, when topics like Triangles, Ratio and Averages are introduced, some students “forget” the basic 4 operations of fractions. Some will forget how to add, subtract, multiply and divide fractions.

If you have to, spend a few periods, days, or even weeks, to drill the basic operations of Fractions. If this is not done, no matter how much effort you put in to teach P5 topics, they will never be able to solve P5 Exam Section C questions, such that they can pass the paper.


3. They are unsure of the 4 operations of decimals -

Like Fractions, some P5 students forget how to work with decimals. They may be unable to work out multiplication and division of decimals. They may also be unable to convert decimals to fractions and vice-versa.

Again if you have to, you need to drill them on this topic.


No Multiplication Tables, Fractions and Decimals, means no pass in PSLE Maths -

Multiplication Tables, Fractions and Decimals are so basic, if the P5 or P6 student does not have these at his fingertips, he would be lucky if he passed PSLE Maths.

Of course, some students may be weak in certain topics like Ratio or Speed. However, as a teacher, you must put the horse before the cart. Get the basics and foundation correct first. Then work on the topics.

Maths is one subject where the student can show as much as a 20 mark increase within just 3 months with close coaching. It may take up more of your time, but it definitely is worth every moment, when you see your students start surprising everyone with such an improvement.

The spin-off of this is that students who improve by such a margin will start believing in themselves. Everything else will then be much easier to deal with.


Point to Ponder –

So what if you do not teach Maths but specialize in English instead? Getting students to improve their English takes a longer time than Maths. But it can be done too.

That will be discussed next week in Part 2 of “How do I motivate my class?”

===========

Update: How do I motivate the class? Part 2

Handling “Section A” Questions for Science

In the post made on 8 Nov 2007, "Why do I keep losing marks for my Science?", we discussed how students can reduce loss of marks in Section B.

In this post, tips on how to minimise loss of marks in Section A will be discussed.

To get an A* for any subject at P5/P6, you will have to have to score above 90% of the maximum mark. To get a Band 1 for any subject at P3/P4, you will have to score at least 85% of the maximum mark. Science is no different.

The good news about science is that 60% (Section A) of your total score is based on Multiple Choice Questions (MCQ). The bad news is that this gives students (and parents) the false impression that Science is an “easy subject”.

What needs to be noted is that MCQ works both ways. You score the 2 full marks if you get the answer right, but get zero, if you get it wrong. There is no “partial mark” like 1 mark or half a mark.

This means that if you get 5 MCQs wrong, you will lose 10% of your marks, making it impossible for you to get that A*, no matter how well you did for your Section B.

A common question structure you will find, is like the example below.

---------
Question -

Which of the following statements about water are false?

(A) It has mass
(B) It has a definite shape
(C) It has no definite volume
(D) It can change from one state to another.

(1) A and D only
(2) B and C only
(3) C and D only
(4) A and B only
----------

Firstly, read the question properly. The question asks “Which of the following statements about water are false?” Many students tend to rush when they answer the question. They do not pay attention to the fact that the question is asking which statements in A,B,C,D are false and not which are true.

Secondly, make a list against the statements by placing a tick against the statement that is true, and placing a cross against the statements that are false. This way you will not be confused so easily.

Illustration


The question asks which of the above are false. By making a list, you have identified that B and C are false. Therefore, the correct choice is (2) – B and C only.

By placing a tick or a cross to identify which statement is true or false, you minimise your chances of making mistakes. This means you will do better for your MCQs in Section A, resulting in higher marks for your overall Science score.

Do not underestimate Section A Science. It may be the key to whether you score an A or an A*.

Remember, 5 MCQs wrong, and that A* will be out of your reach.

=======================

Related Article: Why do I keep losing marks for my Science?

Mathematics – The “Compounding” Subject

Mathematics is considered a “compounding” subject. Foundation topics are introduced at the early stage. Other topics, which are highly dependent on the knowledge of foundation topics, are then introduced at a later stage. This means that if a student does not have a good grasp of earlier topics, he/she will have problems with topics that will be taught later.

For example, if a student does not understand foundation topics like Fractions or Decimals, he/she will have problems with topics like Ratio, Averages, Percentages, Rate etc, which will be introduced later. Maths is hence, called a “compounding” subject because if the student does not know his earlier topics, the problems will start compounding as time goes by.

It is therefore important to know that for a student to do well in Mathematics for his/her PSLE, he/she must have a strong foundation in Mathematics right from the very start, ie – from Primary One. The later the student works towards understanding Maths, the more difficult it would be for him/her to do well in his/her P6 PSLE Maths.

The flip side to this is that a "compounding” subject has benefits. You can use your knowledge attained in past topics to solve questions set for a current topic. Here is one example.

------------------------
Question –

The distance between Town A and Town B is 450 km. A car started from Town A and travelled towards Town B at a speed of 45 km/h. At the same time, a bus started from Town B and travelled towards Town A at a speed of 30 km/h. What was the distance they each travelled when they passed each other?
------------------------

Obviously, the above topic is Speed. You will see that in the above example, you will be able to use a previously taught topic, which is much easier than Speed, to solve the question. In this case, we will use Ratio instead of Speed.




Since the car travelled at 45 km/h and the bus at 30 km/h, the ratio between the distances covered by the car and bus during any same period is 45:30 or 3:2.

This means that 5 units (3 units for car and 2 units for bus) ---> 450 km.

5 units ----- 450 km
1 unit ----- 450 km divided by 5 units = 90km
3 units (car) ----- 3 units x 90 km = 270 km covered by car (Answer)
2 units (bus) ----- 2 units x 90 km = 180 km covered by bus (Answer)

As it can be seen from the above example, although the question is a Speed question, knowledge that has been acquired in the topic of Ratio is used instead. This method is simpler, easier to grasp and has a less tendency on the part of the student to make calculation errors, compared to if knowledge on the topic of Speed had been used instead.

A student who has a strong foundation in earlier topics is definitely much better off than his/her peers who may not have such a foundation. He/she will be able to use his/her knowledge acquired in past topics to help solve questions that are set in current topics.

Maths is a “compounding” subject. You need to have a strong grasp of earlier topics to be able to do well in topics that are taught later.

It is a mistake to think that you can “catch up” with your P3 and P4 Maths, when you are in P5 and P6.

Likewise, it is a mistake to think you can catch up with your P5 Maths, when you are in P6.

The later you start strengthening your foundation in Maths, the more difficult you will find Maths as a subject, when you sit for your PSLE.

Finding out more about the Secondary School of your choice online

Here is a step-by-step guide to find out more about the secondary school of your choice online.

1. Click on this link.

You will be brought to a webpage that will feature this



Under the “Basic Search for Schools”, choose “Secondary Schools” and click on the flag on the right-hand side of the tool bar (circled in bold in the above image), and choose a school.


2. A detailed information on the school you chose will appear as below.


click on image below to enlarge



Scroll down and you will see the PSLE aggregate range of the school for the Year 2006 as shown in the next image. There are links to previous years’ aggregates as well.

click on image below to enlarge



That’s all!

Good luck and wish you the best in getting the school of your choice!

Breakdown of marks allocated for PSLE subjects

Below, is a breakdown of marks that has been allocated for PSLE subjects.

MCQ - Multliple Choice Questions
OE - Open ended questions

.

More on PSLE Aggregate and T-Scores

This post is Part 2 on the topic of PSLE Aggregate and T-Scores. In the last post in this blog , How PSLE Aggregate and T-Scores are calculated, we saw how those scores are calcuated.

One concern parents and students have is that there may be bias towards language subjects because the total score is 200, while the total for Maths and Science is 100.

In this post, we will see that there is no bias towards any particular subject, although the total scores for languages is twice that of Maths and Science.

Below is a tabulation to show that T-score eliminates any bias that may occur due to more total marks allocated to a particular subject.





In the example above, the Raw Score of all subjects for this student is 90%.

English – 90% of 200 marks = 180 marks
MT - 90% of 200 marks = 180 marks
Maths – 90% of 100 marks = 90 marks
Science – 90% of 100 marks = 90 marks


The Average Score of the cohort for all subjects is 50% of the maximum score.

English – 50% of 200 marks = 100 marks
MT - 50% of 200 marks = 100 marks
Maths – 50% of 100 marks = 50 marks
Science – 50% of 100 marks = 50 marks


The Standard Deviation (Std Dev) is 40% from the average.

English – 40% of 100 marks (the average) = 40 marks
MT - 40% of 100 marks (the average) = 40 marks
Maths – 40% of 50 marks (the average) = 20 marks
Science – 40% of 50 marks (the average) = 20 marks


Using the T-score formula 50 + 10(X-Y)/Z, we can note that for all the subjects, the T-Score is 70. Although English and MT have a total score of 200, while Maths and Science have a total score of 100, this is automatically adjusted with the T-Score calculation.

There is no bias towards any subject in the calculation of PSLE Aggregate and T-Scores.

Parents and students need not be unduly worried.

How PSLE Aggregate and T-Scores are calculated

Now that the dust has settled, we can perhaps take a look at the most asked, yet least answered question about the PSLE. That question is –

How are PSLE Aggregate Scores calculated?

To understand how PSLE Aggregate Scores are calculated, we must first understand T-Score. T-Score is the adjusted score a student will get for a subject, after a series of tabulations has been made.

Formula for T-Score


X = Raw score of student
Y = Average Score of the whole cohort
Z = Standard Deviation* (SD)

Standard Deviation* (SD) is the spread of the marks around the average.

Example 1 -
Allan, Bernard and Charles have $45, $50 and $55 respectively. They have an average of $50 each.

Example 2 -
Dan, Edward and Frank have $10, $50 and $90 respectively. They also have an average of $50 each.

In Example 1, the spread ($45 to average of $50 and $55 to average of $50) is smaller than the spread in Example 2, where the spread is bigger ($10 to average of $50 and $90 to average of $50)

As such, Example 1 will have a smaller SD, as compared to Example 2.

A more detailed explanation of how SD is calculated can be found in this link.


Simpler Way to read Standard Deviation (SD)

If the average score of 3000 pupils who sat for Science Test is 50 marks and the SD is 5, it means that 2/3 of the 3000 pupils have scored 5 marks around the average, which means 2000 of the students scored from 45 to 55 marks.

If the average score of the same 3000 pupils who sat for Mathematics Test is 50 marks and the SD is now 10, it means that 2/3 of the 3000 pupils have scored 10 marks around the average, which means 2000 students scored from 40 to 60 marks.


Example of how T-score is calculated

Li Ting’s score for Mathematics – 90 (X)
Average score of cohort – 75 (Y)
Standard Deviation - 20 (Z) (this means 2/3 of cohort scored from 55 to 95)

Using the T-Score formula

T = 50 + 10(X – Y) / Z

T = 50 + 10 x (90 – 75) / 20

= 50 + 10 x 15/20

= 50 + 10 x 0.75

= 57.5

Li Ting’s T-score for Mathematics is 57.5

Now that we have covered T-score, we can take a look at PSLE Aggregate Score.


Using T-Score to Calculate PSLE Aggregate Score

Let’s now take a look at Li Ting’s total performance



The cohort’s average and standard deviation plays a big part in Li Ting’s score. To demonstrate, let’s move the average scores of all subjects down by 10 marks each, keeping all other variables (raw score and SD) constant. This is how Li Ting’s score will now look like.




Take note that Li Ting’s aggregate goes up from 245 to 260 when the averages of all subjects went down by 10 marks each. This shows that if the cohort is weaker, Li Ting’s aggregate score will increase, even if she scores the same marks for all the subjects.

It is therefore not accurate to compare a student’s aggregate score in a particular year, to the aggregate score of another student in a different year. Each year will have a different average for all the subjects.

Parents who have more than 1 child, tend to compare each child’s PSLE Aggregate Score with his/her sibling's score. This is not a very fair comparison.


Final Note –

Because PSLE aggregate score is based on T-scores, theoretically, there is no such thing as “maximum aggregate score”.

Many parents believe the (non-existent) maximum aggregate is 300. That is a misconception.

To demonstrate, I have bumped up Li Ting’s score (in Table 3) to full marks for all her subjects, using the same averages and SDs found in Table 2.




Note that although Li Ting scored 100% marks for all subjects, her PSLE Aggregate Score is only 286. She did not score the (imaginary and non-existent maximum) PSLE Aggregate Score of 300!

The only way to score that 300 (or even above that), is to have a very weak cohort in your year.


So if our imaginary Li Ting scored 100% for all her subjects and still only scored 286 for her PSLE Aggregate, how did Ms Natasha score a PSLE Aggregate of 294 for the year 2007? I don’t have the stats, but my guess is that the averages and SDs of the individual subjects of the cohort played a big role.

In any case, 294 is a respectable score, and we should give credit where it is due. It is an all time high and Ms Natasha definitely deserves the recognition for her outstanding performance.

I hope the article in this post gives parents and students a better picture how PSLE Aggregate Scores are calculated.


=============

Raffles Girls’ Primary School 2005 PSLE Math Prelim Question

A school staged a play at Victoria Theatre on two evenings. On the first evening, there were 80 more boys than girls in the audience. On the second evening, the number of boys decreased by 10% while the number of girls increased by 20%. If there were 1542 boys and girls on the second evening, what was the total sum of money collected from the sale of the tickets on the two evenings if each ticket cost $30?

On 2nd Evening,

90% + 72 (boys) + 120% (girls) ---- 1542

210% + 72 ----- 1542

210% ----- 1542 - 72 = 1470

1% ----- 1470 divided by 210 = 7 (all important 1%)


Total number of children (1st evening + 2nd evening)

100% + 80 (boys, 1st evening) + 100% (girls, 1st evening) + 90% + 72 (boys, 2nd evening) + 120% (girls, 2nd evening)

= 410% + 80 + 72
= (410% x 7) + 152

= 3022


1 ticket cost $3022. Therefore total amount collected for 2 evenings

$30 x 3022 = $90660

Answer: $90600 was collected for both evenings.

Top PSLE student attains highest score in 17 years

Same news from another site. (Channel News Asia)

Top PSLE student attains highest score in 17 years

SINGAPORE: St Hilda's Primary School has produced the top PSLE student this year. Natasha Nabila Muhammad Nasir is also this year's top Malay student. With an aggregate score of 294, the Education Ministry said she has set a record as having achieved the highest marks in the 17 years since the current PSLE system was implemented in 1991.

Top PSLE Student Sets New Record

Top PSLE student sets new record with 294 score

Excerpts:

"A ST HILDA'S Primary pupil has scored a record 294 in the Primary School Leaving Examination (PSLE), beating the previous high of 292 set in 1993.

Natasha Muhamad Nasir, 12, eclipsed the record set by Nanyang Primary's Justin Lau in 1993.

Her score was 'outstanding', said the Singapore Examination and Assessment Board (SEAB) spokesman, as it was a good six points ahead of the next highest
score of 288."

Natasha's parents started her early

"Natasha, who plays the piano and violin and is in the Scrabble club, already has a place in Raffles' Girls Secondary and plans to be a paediatrician in future.

Her parents have left nothing to chance when it comes to bringing up Natasha.

When she was still in her mother's womb, they would would read aloud to her and played music for her to listen.

Her mother, Ms Zahara Osman, 44, quit her flight stewardess job after Natasha was born so that she can give her 'quality time'.

When Natasha was three months old, she bought her an encyclopedia set. By two and a half years, she could read a book on her own.

Ms Zahara and her husband, Mr Muhamad Nasir Atan, 47, a Singapore Airlines technician, live in a five-room Pasir Ris flat, but they volunteered at Gongshang Primary in Tampines to get Natasha a place in the popular school."

PSLE 2007 Results out today

The PSLE 2007 results will be out today.

Press release on 19 November 2007 by The Ministry of Education.

Rosyth School 2006 PSLE Math Prelim Question

Mr and Mrs Wong left their house in the same car for Town P. Mr Wong drove at a speed of 60 km/h. Realizing that he left his lap-top at the home, he let Mrs Wong alight at a bus-stop and drove back to his house. Mrs Wong walked from the bus-stop at a speed of 4 km/h to Town P. It took her 45 min to reach Town P. Both Mr Wong and Mrs Wong arrived at Town P at the same time. Find the distance between their house and Town P.

Solution

(click on image below for clearer view)

Distance (bus-stop to Town P) ---- Speed x time
= 4km/h (Mrs Wong's walking spd) x 3/4h
= 3 km (distance from bus-stop to Town P)


Time for car to travel 3 km at 60 km/h (time = distance/speed)
= (3km) divided by (60 km/h)
= 3 min

Therefore it took Mr Wong 3 min to drive from bus-stop to Town P.

Since Mrs Wong took 45 min to walk from bus-stop to Town P, it also means that Mr Wong took 45 min to travel from bus-stop to their home, and from their home to Town P.

This means that the time Mr Wong took to travel from bus-stop to his home, and from his home to bus-stop again would be -

45 min – 3 min = 42 min


Distance covered by Mr Wong during that 42 min period -

Dist = speed x time

= 60km/h x 42min

= 60km/h x (42/60)h

= 42 km

42 km is the distance from bus-stop to home, then back to bus-stop again.

But distance from home to bus stop is only half of that, which is

1/2 x 42km

= 21 km (distance from home to bus-stop)


Distance from home to Town P therefore is

21 km (distance from home to bus-stop) + 3 km (distance from bus-stop to Town P)

= 24 km

Answer: The distance between their home and Town P is 24 km.

Catholic High School 2006 PSLE Math Prelim Question

The figure below, not shown to scale, is made up of semi-circles and circles. Given that the diameter of the large semicircle is 42 cm, find the area of the shaded region and express your answer as a fraction in the lowest term.

Solution

Area of large semi-circle

1/2 x (22/7) x 21cm x 21cm = 693 square cm


Area of 1 circle (within large semi-circle)

(22/7) x 7cm x 7cm = 154 square cm

Note -
Radius of circle is 7cm because diameter of large semi-circle is 42cm. This diameter is equivalent to the total diameters of the 3 smaller semi-circles at the base of the figure above. Diameter of 1 small semi-circle is therefore 42cm divided by 3 = 14cm. Radius of smaller semi-circle (and circle) is hence, 7 cm.


There are 2 circles and 3 smaller semi-circles in the large semi-circle. This is equivalent to an area of 3.5 circles within the large semi-circle. Therefore,

Area of 3.5 circles (within large semi-circle) is

154 square cm x 3.5 = 539 square cm.


Area of the portion that is inside large semi-circle, but outside the two circles and three small semi-circles is

693 square cm - 539 square cm = 153 square cm


Area of shaded portion is 1/3 the area above, therefore,

154 square cm divided by 3

= 51 and 1/3 square cm (Answer)

Nan Hua Primary School 2006 PSLE Math Prelim Question

Eight identical 5-cm cubes are placed in an empty rectangular tank of length 75cm and width 40cm. The tank is then filled with water running from a tap at the rate of 9 litres per minute. It takes 11 min to fill up 2/3 of the tank.

a) How much more water is needed to fill up the tank to its brim? (Express your answer in litres)
b) Find the height of the tank.


Volume of 1 cube ----- 5cm x 5cm x 5cm = 125 cubic cm.
Volume of 8 cubes ----- 125 cubic cm x 8 = 1000 cubic cm.

In 1 minute ---- 9 litres is filled in the tank.
In 11 mins ----- 99 litres (99 000 cubic cm) will be filled.
By 11 mins, 2/3 of the tank is filled

Volume of 2/3 of tank
99 000 cubic cm (water) + 1000 cubic cm (8 cubes)
= 100 000 cubic cm or 100 litres

Q(a) How much more water is needed to fill up the tank to its brim? (Express your answer in litres)

At 2/3 height of tank ----- 100 litres
At 1/3 height of tank ----- 100 litres divided by 2 = 50 litres

Answer: 50 litres of water more was needed.


Q(b) Find the height of the tank.

Volume of whole tank
100 litres (2/3 volume) + 50 litres (1/3 volume) = 150 litres

Height of tank
Volume = length x width x height
150 litres (150 000 ml) = 75cm x 40cm x height
Height = 150 000ml divided by (75cm x 40cm)
Height = 50cm

Answer: The height of the tank is 50cm.

Red Swastika School P5 CA2 2007 Math Question

Miss Chee bought some pencils, pens and notebooks. The number of notebooks she bought was 25% of the number of pens. The cost of a pencil, a pen and a notebook was $2, $3 and $7 respectively. The total cost of the pens and notebooks were $418 and the total cost of the pencils and notebooks were $262. How many pencils did Miss Chee buy?


Pencils (unknown no. of pencils) ----- ? x $2 each
Pens ----- 4 units x $3 each ---- 12 units (of dollars)
NB ----- 1 unit x $7 each ----- 7 units (of dollars)
("Pens" has been allocated 4 units while "NB" 1 unit because the number of NBs bought is 25% of the number of pens)


Pens + NB ----- $418
12 units + 7 units ---- $418
19 units ----- $418
1 unit ------ $418/19 = $22 (the all important 1 unit)

Pencils + NB ----- $262
? x $2 + 7 units ------ $262
? x $2 + (7 x $22) ----- $262
? x $2 + $154 ----- $262
? x $2 ----- $262 - $154 = $108
? ---- $108/$2 = 54

Answer: She bought 54 pencils

Cloze Shaves and Horrors

Many students and parents find it baffling when it comes to Cloze Comprehension Passages. Quite a fair amount of marks is lost in this section, making it one of the most “worrisome” sections in English Paper 2. So what does a student need to do, in order to minimize loss of marks?

Cloze Passages test the student’s vocabulary, as well as his/her comprehension. Most teachers advise students to read the passage in full, before attempting to answer the questions. This gives the students an idea what the “theme” of the passage is about.

Hence, if the “theme” of the passage is about “hospital”, we can expect words like “nurses”, "doctors", or perhaps, “patients”, “ward”, “wheelchair” and “emergency” to be used.

However, not all passages have clear themes. This may present problems to students who lack a strong vocabulary. The trick is to look at the background and context of the passage. That is why it is important to read the passage in full, before attempting to answer.

Below, is a sample passage. Try it out. This passage has been written such that the opening paragraph gives the reader the “background”. Do not expect this kind of help in actual exams.

In real exams, the blanks start in the very first paragraph. This sample is just to help readers to see the link between the answers and the “background theme”. Hence, a full first paragraph without blanks is given below.


Sample Passage
--------------------
Jake continued his trek in the mountainous forest. He considered himself lucky to be alive. Just days ago, he lost his co-pilot in a horrific crash, when their light aircraft malfunctioned in mid-air. Jake thought he saw death in the face, when their plane came hurtling down. Miraculously, he sustained only a deep gash on his forehead. But he knew the co-pilot was dead when he saw his body pinned under a heap of twisted metal, motionless.

Jake has been _______ (1) in the forest for about a week. He has crossed many streams, but there appears to be no village or settlements around for miles. He knew he was lost and had to find help fast. As he approached a river, he noticed a very tall tree. Jake climbed the tree to _______ (2) for signs of human life or activity. There was none.


------------------

Suggested Answers:

Q(1)
- wandering (highly recommended)
- walking, staying, living, sleeping (unacceptable)

Why “wandering” is preferred – The passage indicates that Jake was on the move. Words like “trek” and “crossed many streams” suggest that Jake was not stationary. Hence, answers that indicate non-movement like “staying” will be considered unacceptable.

“Living” suggests that Jake has made the forest as his place of residence, while “sleeping” is out of context, because the theme is about Jake’s survival and his concerted effort to seek help.

“Walking” too, is unacceptable because “walking” infers “moving to a place in a purposeful manner, with a specific destination in mind”. Example – “I walk to school.” Jake has no specific destination, other than to seek help. Furthermore, “has been walking” may infer Jake has been walking non-stop, for one week.

“Wandering” gives the reader the idea that the person is lost and has covered a wide area, without any specific destination. Example – “We saw the little lost girl wandering in the city.”


Q(2)
- look (highly recommended)
- search (acceptable)
- find (unacceptable)

Why “look” is preferred – “Look” suggests a small area. Example – “I have dropped my pen. I need to look for it under the table.”

“Search” suggests a much wider area. Example – “Rescue workers searched for survivors from the capsized ship.”

Although the passage appears to tell readers that the area is wide (forest), “look” is preferred, because Jake climbed a tree, restricting his mobility and thus reducing the area. Hence, “look for signs” is preferred over “search”.

However, “search” is also acceptable because contextually, Jake was searching for signs of human life even before he climbed the tree, and continued to do so when he climbed that tree.

“Find” is unacceptable because, (1) you need to lose something, before you can “find” it. Example: “Help me find my pen”; or (2) you make what you wish to find an “objective or mission”. Example – “I need to find the truth.”

Furthermore, “find for” is an unacceptable expression. You “find something”, not “find for something”.

--------------------
The above article was published in Excel!, a publication of Excel Eduservice in April 2006.
Publication Permit No: MICA (P) 135/03/2006
All Rights reserved

The Consequential Question Trap

“The challenge, and it is often a difficult one, is for the question setter to pose the question in such a way that pupils with widely different background experiences will all build a sufficiently common mental picture and that mental picture is the same as the question setter’s mental picture” – Associate Prof Boo Hong Kwen, NIE (Straits Times Forum, 15 Oct 2004), commenting on the difficulty level of the PSLE 2004 Science Paper.

Question for students is, do you have a mental picture that is the same as the question setter’s mental picture?

--------------------------------------------

THE CONSEQUENTIAL QUESTION TRAP -
Why you should know what is in the question setter’s mind behind that Science question


Some students are puzzled, why they are marked wrong for certain Science questions, when the answer they give is right. This usually occurs when a set of questions is tied to a certain understanding of a theory.

A typical question (like the one illustrated below), is subdivided into Part (a) and Part (b). In this particular example, Part (a) tests on application of a theory, while Part (b) tests on knowledge of the theory itself.

In such an instance, if Part (a) is answered wrongly, Part (b) will also be marked wrong, regardless if the answer in Part (b) is answered correctly or not. The reason is because if the student gets Part (a) wrong, it tells the examiner that he/she does not understand the topic at all.

As such, even if Part (b) is answered correctly, it simply gives the examiner the impression that the student has probably just memorised the answer by heart, without understanding the theory involved.

Such a question is dubbed, The “Consequential Question Trap". It is considered a “trap” because students who learn science “by heart”, will usually fall for this kind of “trap” questions.

Below is an example of a typical “consequential question”, where Part (b) is dependent on Part (a). This example is a question taken from Primary 5 syllabus. The topic is “Electricity”.

--------------------------
Question
The diagram below shows four objects A, B, C and D connected to an electric circuit.



a) Which bulb(s) will light up?
b) What conclusion can you give regarding objects A, B, C and D?

Answer:
a) Bulbs 1, 2 and 4 only.
b) Steel rod and metal rulers are conductors of electricity, while rubber and plastic rods are not.
-------------------------

Part (a) tests the student’s application of theory, as to what are the consequences if you place a conductor or an insulator in an electrical circuit.

Part (b) tests on student’s knowledge on the characteristics of conductors and insulators.

To be able to answer Part (b) correctly, you must be able to identify which bulbs light up in Part (a).

If the student gets Part (a) wrong, it gives examiners the idea that he/she does not understand that the conductors will form a closed electrical circuit, resulting Bulbs 1, 2 and 4 to light up - while insulators will break the circuit, causing Bulb 3 to remain unlit.

From here, we can see that if Part (a) is answered wrongly, and if the student proceeds to answer Part (b) correctly, the impression given to examiners is that, the student has probably learnt by heart that “metals are conductors of electricity while plastic and rubber are not” in Part (b) - without understanding the theory that conductors conduct electricity, while insulators break the electrical circuit.

The above being the case, examiners will be highly suspicious as to how the student answered Part (b) correctly, when Part (a) has been answered wrongly!

A “consequential question” hence, has to be answered correctly from the start. If the initial part is answered wrongly, the subsequent answer(s) will be marked wrong, regardless how they have been answered.

The only way to get all parts right, is to study and understand its theory.

Learning “by heart” will not help!
---------------------------------------------
The above article was published in Excel!, a publication of Excel Eduservice in Oct 2004.
Publication Permit No: MITA (P) 297/03/2004
All rights reserved

Fuhua Primary School PSLE Math Prelim 2007 Question

Emily bought a book. On the first day, the number of pages of the book read was 25% of the number of pages unread. On the second day, she read another 55 pages of the book. As a result, the number of pages she read was 80% of the number of pages unread. How many pages did the book have?

Solution -
(click on image below to enlarge)



From the above image,

1st day ----- she read 1/5 of whole book

2nd day ----- she read 4/9 of whole book


Difference between 1st and 2nd days

*4/9 – 1/ 5 (of book) ----- 11/45 of book (read on 2nd day)

11/45 ----- 55 pages

1/45 ----- 55 divided by 11 = 5 pages

45/45 ----- 45 x 5 pages = 225 pages

Answer: The book had 225 pages.

*Italics in blue was amended on 14 Jan 2009 to correct typo error.

Raffles Girls’ Primary School P5 SA1 2007 Math Question

Adam and Ben each have some money. If Adam spends $4, the ratio of the amount of money Adam has to the amount that Ben has will be 3:5. If Ben spends $4, the ratio of the amount of money Adam has to the amount that Ben has will be 11:13. How much money does each boy have?


(click on image to enlarge)


- If Adam spends $4, the ratio of the amount of money Adam has to the amount that Ben has will be 3:5, hence,

Adam has 3 units (after $4 spent), while Ben has 5 units (marked in blue in illustration above).


- If Ben spends $4, the ratio of the amount of money Adam has to the amount that Ben has will be 11:13, hence,

Adam now has been allocated 11 parts, while Ben has been allocated 13 parts (after $4 spent by Ben), as marked in red in llustration above.


From here, we can deduce

2 units ----- $4 + 2 parts $4
2 units ----- $8 + 2 parts
1 unit ----- $4 + 1 parts
3 units ----- $12 + 3 parts (*)


However, we know that
(Adam) 3 units ----- 11 parts - $4 (#) (as from model above)


Both * and # have an equivalent of 3 units. Therefore,

$12 + 3 parts (*) ----- 11 parts - $4 (#)
$16 ----- 8 parts
1 part ----- $16 divided by 8 = $2


Adam has ---- 11 parts
= (11 parts x $2)
= $22

Ben has ----- 13 parts + $4
= (13 parts x $2) + $4
= $26 + $4
= $30

Answer: Adam has $22, while Ben has $30.

The Use of the Past Tense

Dear Students,

Writing well is important. For English, examiners give marks based on what you write in your exam paper. If you cannot write, you cannot score. Simple as that. Therefore, learn your tenses well! Good luck!

Most essays are required to be written in the Past Tense. As such, it is important to know how to use the Past Tense appropriately. In the English Language, there are six different tenses that can be used when we write about the past. They are:

-----
Simple Past
Past Progressive
Simple Present Perfect
Present Perfect Progressive
Simple Past Perfect
Past Perfect Progressive
-----

In Primary school, the two most important Past Tenses are the Simple Past and Progressive Past.


- Simple Past - This form is used when we talk about past event(s) that happened quickly or over a long period.

Example of past event that happened quickly
– “Last night I saw the eclipse of the moon.”

Example of past event that happened over a long period
– “I spent my whole childhood Singapore.”


- Progressive Past – This form is used when you want to say something that happened around a particular time.

Examples –
“What were you doing at nine o’clock last night?”
“I was watching the news on TV.”


Combining Simple Past and Progressive Past in one sentence
- can you spot the difference?

Example 1 - As I was walking to school, it started to rain.
Example 2 - While it was raining, I walked to school.


Question – Which happened first? Did it rain first, or did I start walking first?

Example 1 - As I was walking to school, it started to rain.

Example 2 - While it was raining, I walked to school.



In Example 1, I walked before it started to rain.

In Example 2, it rained before I started to walk.

The action that happens first is in the Progressive Past, while the second action that interrupts the first action, is in the Simple Past.


A student who is able to include both the Simple Past and Past Progressive in one sentence, increases his/her chances of a higher score in his/her Composition, compared to another student, who writes with just one tense per sentence. Below is an illustration how you can enhance your essay writing.

Instead of writing….
The police officer and the robber struggled. Suddenly a shot rang out.

Try this…..
While both the police officer and the robber were struggling furiously, a shot rang out.

Instead of this....
We walked down the hall. Suddenly we heard an ear-piercing scream.

Try this....
We were walking nervously down the hall when suddenly, we heard an ear-piercing scream.

Practice makes perfect. Practise your tenses through reading and writing.

===============

The above article was published in Excel!, a publication of Excel Eduservice, in July 2004.
(Publication Permit No: MITA (P) 297/03/2004)
All rights reserved.

Why do I keep losing marks for my Science?

That appears to be a very common question among students. Very often, they are puzzled why their friends are able to score 2 marks for a question, while they score only 1 or half mark, for what appears to be very similar answers given.

To understand how a student scores or loses marks, you must understand exactly what the examiner looks for, when he or she is marking the exam paper. Since most marks are lost in Section B, in this post, we will touch on Section B type questions only.


An examiner looks for two things in an answer, when he or she marks Section B questions. They are:

1. Key word(s)
2. Key concept(s)

Key word is the word that forms the main answer. This word tells the examiner if the student knows his or her work. If the key word is missing in the answer, the examiner will doubt that the student knows his or her work.

Key concept is the explanation of the concept that has been applied in the answer. It tells the examiner if the student understands the theory, concept and its application. If the key concept is missing in the answer, the examiner will believe that although the student has the answer, he or she does not have a full understanding of the concept(s) involved.

Below, is a Sample Question, followed by a Sample Answer.

==========================
Question - Raju put some ice into a glass of water. After a while, he noticed that water droplets started to appear on the outside of the glass. What caused the droplets of water to form?
(2 marks)





Sample Answer

When the water vapour in the air comes in contact with the cold surface of the glass, condensation takes place and water droplets are formed on the outside of the glass.
=========================

In the sample answer above, the key word is in red, while the key concept is in blue. The above answer is sufficient to score the 2 full marks.

The key word here is “condensation”. Without this word, it makes it very difficult for the examiner to give the student any mark, let alone full marks. This is because if “condensation” is missing, it tells the examiner that the student does not know what has been asked.

The key concept on the other hand, tells the examiner that the student knows that condensation has taken place, and more importantly, tells the examiner that the student knows under what conditions condensation takes place.

Hence, this question tests on knowledge (what is condensation) and understanding (how condensation changes the state of water and under what circumstances these changes will take place).

If the student simply answers “condensation” without further explanation, he/she will get less than 2 marks.

If the student explains the process of condensation, without mentioning the word “condensation”, then it all depends how convinced the examiner(s) is/are, that the student has understood the concept of condensation, by studying the answer given. However, more often than not, examiners will not be convinced.

Having mentioned that, even if the student does manage to convince the examiner(s), he/she will still not get the 2 full marks.

The student must give both, the key word and the key concept, to score full marks.

=======================================
The above article was published in Excel!, a publication of Excel Eduservice, in March 2006.
(Publication Permit No: MICA (P) 135/03/2006)
All rights reserved.
=======================================

Related article: Handling “Section A” Questions for Science

Pei Chun Public School PSLE Math Prelim 2007 Question

Rectangles X and Y are overlapped as shown in the figure below. The ratio of the area of the rectangle X to that of rectangle Y is 3 : 5. The ratio of the unshaded area of rectangle X to the unshaded area of rectangle Y is 1 : 3. The dimension of rectangle X is 6cm by 4cm.

(a) What is the area of the shaded part?
(b) What is the fraction of the area of the shaded part to that of the whole figure?



Working Solution -

The ratio of the unshaded area of rectangle X to the unshaded area of rectangle Y is 1 : 3. Hence, we label 1 unit for unshaded area of rectangle X and 3 units for unshaded area of rectangle Y as shown below.


We also know that the ratio of the area of rectangle X to that of rectangle Y is 3 : 5

For area of rectangle X to that of rectangle Y to be 3 : 5, the shaded area has to be 2 units as illustrated in the figure below.



We also know that Area of Rectangle X is

6 cm (length) x 4 cm (breadth) = 24 square centimetres.

Ratio of Area of rectangle X to that of Area of rectangle Y is 3 : 5

(Area X) is 3 units ----- 24 square centimetres.

1 unit ----- 24 square centimetres divided by 3 = 8 square centimetres.
(The all important 1 unit)



Q(a) What is the area of the shaded part?

Area of shaded part is
2 units ------- 8 square centimetres x 2 = 16 square centimetres

Answer: The area of the shaded part is 16 square centimetres.



Q(b) What is the fraction of the area of the shaded part to that of the whole figure?

Shaded part ----- 2 units
Whole figure ------ 1 unit (unshaded part of rectangle X) + 3 units (unshaded part of rectangle Y) + 2 units (shaded part) = 6 units

Area of unshaded part / Area of whole figure.

2 units / 6 units = 1/3

Answer: The fraction of the area of the shaded part to that of the whole figure is 1/3.

Singapore Chinese Girls School PSLE Math Prelim 2007 Question

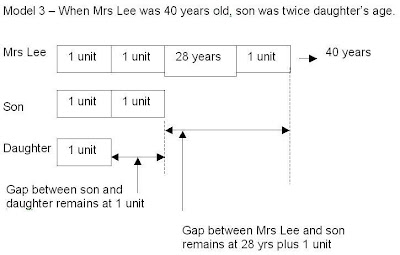
When Mrs Lee was 40 years old, her son was twice her daughter’s age. Mrs Lee will be twice her son’s age when her daughter is 28 years old. How old will Mrs Lee be when her daughter is 20 years old?


When Mrs Lee was 40 years old, son was twice daughter’s age.

Model 1 (click on image below for clearer view)



When daughter turns 28 years old, Mrs Lee will be twice son’s age.

Model 2 (click on image below for clearer view)



Now that we know

- Mrs Lee is 28 years plus 1 unit older than son
- Son is 1 unit older than daughter

we can draw the next model when Mrs Lee was 40 years old again.


Model 3 (click on image for clearer view)



From Model 3 we can work out

(Mrs Lee) 3 units + 28 yrs ---- 40 yrs

3 units ----- 40 years - 28 years
3 units ----- 12 years

1 unit ---- 12 years divided by 3
1 unit ---- 4 years (the all important 1 unit)


Finally, we can work out Mrs Lee's age when her daughter turns 20 years old.

Model 4 (click on image for clearer view)



When daughter turns 20 years old, Mrs Lee will be -

20 years (daughter’s age) + 4 years (gap between daughter and son) + 28 years + 4 years (gap between Mrs Lee and son)

20 years + 4 years + 28 years + 4 years = 56 years.


Answer: Mrs Lee will be 56 years old when her daughter turns 20 years old.

Nanyang Primary School 2007 PSLE Math Prelim Question

At a school carnival, there were 520 more girls than boys. 1/8 of the girls and 20% of the boys left the carnival. In the end, there were 488 more girls than boys.

(a) Did more girls or boys leave the carnival? How many more?
(b) How many children were there at the carnival in the end?

Click on image below to enlarge.



Before anyone left,

Girls - 1 unit + 520
Boys - 1 unit

After some boys and girls left, there were 488 more girls than boys.

But we know from the above model (marked in red) that
Girls remained at carnival ------- 7/8 unit + 455
Boys remained at carnival -------- 4/5 unit.


(Girls remained) – (Boys remained) = 488 more girls than boys

(7/8 unit + 455) – (4/5 unit) ---- 488

7/8 unit - 4/5 unit + 455 ---- 488

3/40 unit ----- 488 – 455

3/40 unit ----- 33

1 unit ---- 33 divided by 3/40

1 unit ---- 440 (the all important 1 unit)



Question (a) - Did more girls or boys leave the carnival? How many more?

Girls left carnival -------- 1/8 unit + 65

1/8 x 440 + 65 = 120 girls left.


Boys left carnival -------- 1/5 unit

1/5 x 440 = 88 boys left.


120 (girls) – 88 (boys) = 32 more girls than boys.


Answer for (a): 32 more girls than boys left the carnival.



Question (b) - How many children were there at the carnival in the end?

Girls remained at carnival ------- 7/8 unit + 455

7/8 x 440 + 455 = 840


Boys remained at carnival -------- 4/5 unit

4/5 x 440 = 352


Total remained ------ 840 (girls) + 352 (boys) = 1192 (children)


Answer for (b): There were 1192 children who remained at the carnival.